‘The importance of understanding your errors’
30th April 2024
‘A Technical Insight’. Author: Christopher (Chris). J. Parker MEng(Hons), CEng MIMechE, fCMgr MCMI, AMInstR

Errors are common in engineering problems even if we don’t acknowledge them. They usually stem from assumption values at the onset of tackling a problem. Today, my aim is increase your awareness of calculation errors, and prompt you to question whether they are acceptable or not. If they are not acceptable, an alternative method should be applied, but also be aware new errors may be incurred!
To start with, contemplate the following question:
How much energy is needed to raise the temperature of 1 litre of water from 20°C to its boiling point?
This is a run of the mill question any engineer should be able to answer. You will likely default to the specific heat capacity equation where Q = mCP, (T2, and T1 ) Q, m, CP, T2, and T1 are energy, mass, specific heat capacity at constant pressure, final temperature, and initial temperature respectively.
To determine the mass of water, you will also likely use the common knowledge assumptions that the density of water is equal to 1,000 kg/m3, allowing us to convert the 1 litre volume to 1 kg mass and that the boiling point of water is 100°C. A quick Google search reveals a specific heat capacity for water to be 4,200 J/kg.K.
Plugging in all our figures returns an energy input equal to 336,000 J. Straight forward, but how much error have we accepted? Yes, error.
Firstly, a fluid’s density and specific heat capacity values are not constant but are rather variable with respect to pressure and temperature. So far, pressure has not been discussed. The standard atmospheric pressure (SAP) accepted by the scientific community is 101,325 Pa, often referred to as standard atmospheric pressure at sea level. For calculations where pressure is critical, the standard atmospheric pressure is adjusted for altitude changes. Using REFPROP as the authoritative source for our fluid properties, we can find the density and specific heat capacity of water at 20°C and 101,325 Pa is 998.2 kg/m3 (1.dp) and 4,184.1 J/kg.K (1.d.p) respectively. We can also find water’s boiling point at these conditions is 99.97°C (2.d.p). Plugging these values (not rounded) into the previous equation returns 334,017 J, a 0.6% difference. While not a monumental difference, we are starting to discover errors in our original calculation.
Now lets consider the impact altitude changes have on our calculation. The town La Rinconada in Peru, is the highest permanent settlement in the world at approximately 5,000 m above sea level. Here the standard atmospheric pressure is approximately 52,918 Pa, 52% of the sea level value. The impact on our fluid properties is shown next to the sea level pressure in the following table.
| Property | Sea-level | La Rinconada |
| Density at 20°C | 998.2 kg/m3 | 998.2 kg/m3 |
| Specific Heat Capacity at 20°C | 4,184.1 J/kg.K | 4,184.2 J/kg.K |
| Boiling Point | 99.97°C | 82.74°C |
| Density at Boiling Point | 958.4 kg/m3 | 970.0 kg/m3 |
| Specific Heat Capacity at Boiling Point | 4,215.6 J/kg.K | 4,199.0 J/kg.K |
The energy calculation results for the respective locations are listed in the following table.
| Property Condition Source | Sea-level | La Rinconada |
| Common Knowledge Assumption | 336,000 J | 336,000 J |
| REFPROP Initial Condition Bias | 334,017 J | 262,025 J |
As shown in the above table, not accounting for the pressure changes can have a significant difference in the end values and introduce meaningful errors.
So far, we have learned that the standard approach to the seemingly straight forward question does introduce calculation errors, however minor, depending on how the property values are sourced. Before we consider the larger impact for different fluids, I wanted to illustrate the more accurate method to determine the required energy input.
We have already established that the density and specific heat capacity of the fluid changes with temperature and pressure. During the heating process, if we assume a fixed pressure, we can find the energy change per kelvin of temperature increase. Mathematically, this is known as “Riemann sum” and is used to approximate the area under curves. By Using REFPROP to calculate the fluid properties at each kelvin temperature rise (or finer resolution if desired) the energy required for individual temperature rises can be calculated, the sum of which will be the more accurate value.
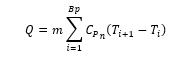
For our water question, the total energy input is calculated to be 334,432 J, very close to the initial condition bias calculated value. The sum total error introduced by our initial calculation with common knowledge assumptions is a huge 0.5%. Perhaps not huge, but very illustrative of why we like to use water as a standard test substance. At this fixed pressure, the density of water across its liquid temperature range does not vary greatly minimising introduced errors. But what if we considered a different substance?
If we change the fluid to ethanol, a type of alcohol, the errors can no longer be ignored. A quick Google search reveals the following fluid properties one would initially assume:
| Property | Value |
| Density | 789 kg/m3 |
| Specific Heat Capacity | 2,460 J/kg.K |
| Boiling Point | 78.37°C |
Following the same process we described for water, we calculate the following values:
| Calculation | Values | Percentage Difference From Googled Inputs |
| Googled Assumed Inputs | 113,293 J | 0 |
| REFPROP Calculated Initial Condition Bias | 110,498 J | -2% |
| REFPROP Variable Properties per Kelvin | 122,153 J | +8% |
An 8% difference, an error I would consider significant and would prompt me to question the validity of the initial calculation. While in the relatively small energy quantities we are dealing with the impact in minor, for larger applications 8% can have major design implications. But what applications does ethanol have in this scenario? Truthfully, I don’t know, I am just using it to illustrate the error impact alternative fluids have on the specific heat capacity equation. With new chemicals being formulated for thermal applications, we can investigate the bespoke properties and determine how much error is introduced.
When you’re next faced with a mathematical problem, not just thermodynamics related, please consider the generated errors and question whether they are acceptable for the application. At WAVE we consider overlooked details like this in all our work to aid important design choices.



